Civil Engineering Material

STEEL
Steel is the common name for a large family of iron alloys which are easily malleable after the molten stage. Steels are commonly made from iron ore, coal, and limestone. When these raw materials are put into the blast furnace, the result is a "pig iron" which has a composition of iron, carbon, manganese, sulfur, phosphorus, and silicon.

As pig iron is hard and brittle, steelmakers must refine the material by purifying it and then adding other elements to strengthen the material. The steel is next deoxidized by a carbon and oxygen reaction. A strongly deoxidized steel is called "killed", and a lesser degrees of deoxodized steels are called "semikilled", "capped", and "rimmed".

Steels can either be cast directly to shape, or into ingots which are reheated and hot worked into a wrought shape by forging, extrusion, rolling, or other processes. Wrought steels are the most common engineering material used, and come in a variety of forms with different finishes and properties.

Standard Steels

According to the chemical compositions, standard steels can be classified into three major groups: carbon steels, alloy steels, and stainless steels: Steels Compositions Carbon Steels Alloying elements do not exceed these limits: 1% carbon, 0.6% copper, 1.65% manganese, 0.4% phosphorus, 0.6% silicon, and 0.05% sulfur. Alloy Steels Steels that exceed the element limits for carbon steels. Also includes steels that contain elements not found in carbon steels such as nickel, chromium (up to 3.99%), cobalt, etc. Stainless Steels Contains at least 10% chromium, with or without other elements. Based on the structures, stainless steels can be grouped into three grades: Austenitic: Typically contains 18% chromium and 8% nickel and is widely known as 18-8. Nonmagnetic in annealed condition, this grade can only be hardened by cold working. Ferritic: Contains very little nickel and either 17% chromium or 12% chromium with other elements such as aluminum or titanium. Always magnetic, this grade can be hardened only by cold working. Martensitic: Typically contains 12% chromium and no nickel. This grade is magnetic and can be hardened by heat treatment.

Top of Page

Tool Steels

Tool steels typically have excess carbides (carbon alloys) which make them hard and wear-resistant. Most tool steels are used in a heat-treated state, generally hardened and tempered. There are a number of categories assigned by AISI (American Iron and Steel Institute), each with an identifying letter: W: Water-Hardening S: Shock-Resisting O: Cold-Work (Oil-Hardening) A: Cold-Work (Medium-Alloy, Air-Hardening) D: Cold-Work (High-Carbon, High-Chromium) L: Low-Alloy F: Carbon-Tungsten P: P1-P19: Low-Carbon Mold Steels P20-P39: Other Mold Steels H: H1-H19: Chromium-Base Hot Work H20-H29: Tungsten-Base Hot Work H40-H59: Molybdenum-Base Hot Work T: High-Speed (Tungsten-Base) M: High-Speed (Molybdenum-Base)

General Information

Carbon steels are steels whose alloying elements do not exceed the following limits: Element Max weight % C 1.00 Cu 0.60 Mn 1.65 P 0.40 Si 0.60 S 0.05

Designation

Carbon steels are designated by distinct AISI (American Iron and Steel Institute) four-digit numbers. The first two digits indicate the grades of the steels, while the last two digits give the nominal carbon content of the alloy in hundredths of a percent. Here is an example: XX :0.xx% average carbon content AISI 10 60 10 :Nonresulfurized grades 11 :Resulfurized grades 12 :Resulfurized and rephosphorized grades 15 :Nonsulfurized grades; max Mn content > 1% If a letter L or B shows up between the second and third digits of an AISI number, it means that this grade is either a Leaded steel or a Boron steel; Sometimes a suffix H is attached to a AISI number to indicate that the steel has been produced to prescribed hardenability limits. Examples are: Leaded steels :AISI 12L14, AISI 12L15... Boron steels :AISI 15B48H... H-steels :AISI 1038H, AISI 15B48H...

Alloy steels comprise a wide variety of steels which have compositions that exceed the limitations of C, Mn, Ni, Mo, Cr, Va, Si, and B which have been set for carbon steels. However, steels containing more than 3.99% chromium are classified differently as stainless and tool steels. Alloy steels are always killed, but can use unique deoxidization or melting processes for specific applications. Alloy steels are generally more responsive to heat and mechanical treatments than carbon steels.

AISI Designation

Typically, alloy steels are designated by distinct AISI (American Iron and Steel Institute) four-digit numbers. The first two digits indicate the leading alloying elements, while the last two digits give the nominal carbon content of the alloy in hundredths of a percent. Occasionally we see five-digit designations where the last three digits tell that the carbon is actually over 1%. Here is an example: XXX :x.xx% average carbon content 51 100 13 xx:1.75Mn Manganese 23 xx:3.50Ni Nickel 31 xx:1.25Ni, 0.65-0.80Cr Nickel-Chromium 40 xx:0.20-0.25Mo Molybdenum 44 xx:0.40-0.52Mo 41 xx:0.50-0.95Cr, 0.12-0.30Mo Chromium-Molybdenum 46 xx:0.85-1.82Ni, 0.20-0.25Mo Nickel-Molybdenum 48 xx:3.5Ni, 0.25Mo 50 xx:0.27-0.65Cr Chromium 51 xx:0.80-1.05Cr 50 xxx:0.50Cr, 1.00C 51 xxx:1.02Cr, 1.00C 52 xxx:1.45Cr, 1.00C 61 xx:0.60-0.95Cr, 0.10-0.15V Chromium-Vanadium 92 xx:1.4-2Si, 0.65-0.85Mn, <0.65cr Silicon-Manganese 43 xx:1.82Ni, 0.50-0.80Cr, 0.25Mo Nickel-Chromium-Molybdenum 47 xx:1.05Ni, 0.45Cr, 0.20-0.35Mo 81 xx:0.30Ni, 0.40Cr, 0.12Mo 86 xx:0.55Ni, 0.50Cr, 0.25Mo 87 xx:0.55Ni, 0.50Cr, 0.25Mo 88 xx:0.55Ni, 0.50Cr, 0.20-0.35Mo 93 xx:3.25Ni, 1.20Cr, 0.12Mo 94 xx:0.45Ni, 0.40Cr, 0.12Mo If a B shows up between the second and third digits of an AISI number, it means that this grade is a Boron steel; Sometimes a suffix H is attached to a AISI number to indicate that the steel has been produced to prescribed hardenability limits.

General Information

Stainless steels are high-alloy steels that have superior corrosion resistance than other steels because they contain large amounts of chromium. Stainless steels can contain anywhere from 4-30 percent chromium, however most contain around 10 percent. Stainless steels can be divided into three basic groups based on their crystalline structure: austenitic, ferritic, and martensitic. Another group of stainless steels known as precipitation-hardened steels are a combination of austenitic and martensitic steels. Below are the general compositional contents of these groups.

Grades

Ferritic grades: Ferritic stainless steels are magnetic non heat-treatable steels that contain chromium but not nickel. They have good heat and corrosion resistance, in particular sea water, and good resistance to stress-corrosion cracking. Their mechanical properties are not as strong as the austenitic grades, however they have better decorative appeal. Martensitic grades: Martensitic grades are magnetic and can be heat-treated by quenching or tempering. They contain chromium but usually contain no nickel, except for 2 grades. Martensitic steels are not as corrosive resistant as austenitic or ferritic grades, but their hardness levels are among the highest of the all the stainless steels. Austenitic grades: Austenitic stainless steels are non-magnetic non heat-treatable steels that are usually annealed and cold worked. Some austenitic steels tend to become slightly magnetic after cold working. Austenitic steels have excellent corrosion and heat resistance with good mechanical properties over a wide range of temperatures. There are two subclasses of austenitic stainless steels: chromium-nickel and chromium-manganese-low nickel steels. Chromium-nickel steels are the most general widely used steels and are also known as 18-8(Cr-Ni) steels. The chromium nickel ratio can be modified to improve formability; carbon content can be reduced to improve intergranular corrosion resistance. Molybdenum can be added to improve corrosion resistance; additionally the Cr-Ni content can be increased.

CORROSION

Corrosion Fundamentals

Corrosion is a natural process that seeks to reduce the binding energy in metals. The end result of corrosion involves a metal atom M being oxidized, whereby it loses one or more electrons and leaves the bulk metal, M Mm+ + m e- The lost electrons are conducted through the bulk metal to another site where they reduce (i.e. combine with) a non-metallic element N or another metallic ion G+ that is in contact with the bulk metal, N + n e- Nn- Gm+ + m e- G In corrosion parlance, the site where metal atoms lose electrons is called the anode, and the site where electrons are transfered to the reducing species is called the cathode. These sites can be located close to each other on the metal's surface, or far apart depending on the circumstances. Anode/cathode pairs, known as corrosion cells, come in a variety of forms including composition cells (also known as Galvanic Cells), stress cells, and concentration cells.

Electrolytes and the Corrosion Circuit

Corrosion is essentially an electric circuit, since there is a flow of current between the cathode and anode sites. In order for a current to flow, Kirchoff's circuit laws require that a circuit be closed and that there exists a driving potential (or voltage). Part of the corrosion circuit is the base metal itself; the rest of the circuit exists in an external conductive solution (i.e. an electrolyte) that must be in contact with the metal. This electrolyte serves to take away the oxidized metal ions from the anode and provide reduction species (either nonmetalic atoms or metallic ions) to the cathode. Both the cathode and anode sites must be immersed in the same electrolyte for the corrosion circuit to be complete. The most common electrolyte associated with corrosion is ordinary water. What provides the potential that drives the corrosion circuit? In most cases, the differences in the atom binding energies within a metal provide the driving potential (e.g. composition cells, stress cells). Ion concentration gradients in the electrolyte can also provide a potential (concentration cells). Note that inside the metal, the charge carriers are electrons; outside the metal, the charge carriers are ions dissolved in the electrolyte.

Armstrong number

Armstrong number

In number theory, a narcissistic number or pluperfect digital invariant (PPDI) or Armstrong number^[4] is a number that in a given base is the sum of its own digits to the power of the number of digits.

To put it algebraically, let be an integer with representation d_kd_{k − 1}...d₁ in base-b notation. If then n is a narcisstic number. For example, the decimal (Base 10) number 153 has three digits and is a narcissistic number, because:

If the constraint that the power must equal the number of digits is dropped, so that for some m it happens that then n is called a perfect digital invariant or PDI.^[5][2] For example, the decimal number 4150 has four digits and is the sum of the fifth powers of its digits

so it is a perfect digital invariant but not a narcissistic number.

In "A Mathematician's Apology", G. H. Hardy wrote:

There are just four numbers, after unity, which are the sums of the cubes of their digits:

153 = 1³ + 5³ + 3³

370 = 3³ + 7³ + 0³

371 = 3³ + 7³ + 1³

407 = 4³ + 0³ + 7³.

These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals to the mathematician.

Narcissistic numbers in various bases

The sequence of "base 10" narcissistic numbers starts: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474 ... (sequence A005188 in OEIS)

The sequence of "base 3" narcissistic numbers starts: 0,1,2,12,122

The sequence of "base 4" narcissistic numbers starts: 0,1,2,3,313

The number of narcissistic numbers in a given base is finite, since the maximum possible sum of the kth powers of a k digit number in base b is

and if k is large enough then

in which case no base b narcissistic number can have k or more digits.

There are 88 narcissistic numbers in base 10, of which the largest is

115,132,219,018,763,992,565,095,597,973,971,522,401

with 39 digits.

Unlike narcissistic numbers, no upper bound can be determined for the size of PDIs in a given base, and it is not currently known whether or not the number of PDIs for an arbitrary base is finite or infinite.

Related concepts

The term "narcissistic number" is sometimes used in a wider sense to mean a number that is equal to any mathematical manipulation of its own digits. With this wider definition narcisstic numbers include:

• Constant base numbers : for some m.

• Perfect digit-to-digit invariants :

• Ascending power numbers :

• Friedman numbers

• Sum-product numbers :

• Dudeney numbers :

• Factorions :

where d_i are the digits of n in some base.

Program CODE for FORTRAN

PROGRAM  Armstrong Number

  IMPLICIT  NONE



  INTEGER :: a, b, c                   ! the three digits

  INTEGER :: abc, a3b3c3               ! the number and its cubic sum

  INTEGER :: Count                     ! a counter



  Count = 0

  DO a = 0, 9                          ! for the left most digit

     DO b = 0, 9                       !   for the middle digit

        DO c = 0, 9                    !     for the right most digit

           abc    = a*100 + b*10 + c   !        the number

           a3b3c3 = a**3 + b**3 + c**3 !        the sum of cubes

           IF (abc == a3b3c3) THEN     !        if they are equal

              Count = Count + 1        !           count and display it

              WRITE(*,*)  'Armstrong number ', Count, ': ', abc

           END IF

        END DO

     END DO

  END DO



END PROGRAM  ArmstrongNumber

Perfect number

In mathematics, a perfect number is defined as a positive integer which is the sum of its proper positive divisors, that is, the sum of the positive divisors excluding the number itself. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself), or σ(n) = 2n.

The first perfect number is 6, because 1, 2, and 3 are its proper positive divisors, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) / 2 = 6.

The next perfect number is 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128

Even perfect numbers

Euclid discovered that the first four perfect numbers are generated by the formula 2ⁿ⁻¹(2ⁿ − 1):

for n = 2: 2¹(2² − 1) = 6

for n = 3: 2²(2³ − 1) = 28

for n = 5: 2⁴(2⁵ − 1) = 496

for n = 7: 2⁶(2⁷ − 1) = 8128.

Noticing that 2ⁿ − 1 is a prime number in each instance, Euclid proved that the formula 2ⁿ⁻¹(2ⁿ − 1) gives an even perfect number whenever 2ⁿ − 1 is prime (Euclid, Prop. IX.36).

Ancient mathematicians made many assumptions about perfect numbers based on the four they knew, but most of those assumptions would later prove to be incorrect. One of these assumptions was that since 2, 3, 5, and 7 are precisely the first four primes, the fifth perfect number would be obtained when n = 11, the fifth prime. However, 2¹¹ − 1 = 2047 = 23 × 89 is not prime and therefore n = 11 does not yield a perfect number. Two other wrong assumptions were:

• The fifth perfect number would have five digits in base 10 since the first four had 1, 2, 3, and 4 digits respectively.
• The perfect numbers' final digits would go 6, 8, 6, 8, alternately.

The fifth perfect number (33550336 = 2¹²(2¹³ − 1)) has 8 digits, thus refuting the first assumption. For the second assumption, the fifth perfect number indeed ends with a 6. However, the sixth (8 589 869 056) also ends in a 6. It is straightforward to show that the last digit of any even perfect number must be 6 or 8.

In order for 2ⁿ − 1 to be prime, it is necessary but not sufficient that n should be prime. Prime numbers of the form 2ⁿ − 1 are known as Mersenne primes, after the seventeenth-century monk Marin Mersenne, who studied number theory and perfect numbers.

Over a millennium after Euclid, Ibn al-Haytham (Alhazen) circa 1000 AD realized that every even perfect number is of the form 2ⁿ⁻¹(2ⁿ − 1) where 2ⁿ − 1 is prime, but he was not able to prove this result.It was not until the 18th century that Leonhard Euler proved that the formula 2ⁿ⁻¹(2ⁿ − 1) will yield all the even perfect numbers. Thus, there is a concrete one-to-one association between even perfect numbers and Mersenne primes. This result is often referred to as the Euclid-Euler Theorem. As of September 2008, only 46 Mersenne primes are known,^[2] which means there are 46 perfect numbers known, the largest being 2^43,112,608 × (2^43,112,609 − 1) with 25,956,377 digits.

The first 39 even perfect numbers are 2ⁿ⁻¹(2ⁿ − 1) for

n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917 (sequence A000043 in OEIS).

The other 7 known are for n = 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 43112609. It is not known whether there are others between them.

It is still uncertain whether there are infinitely many Mersenne primes and perfect numbers. The search for new Mersenne primes is the goal of the GIMPS distributed computing project.

Since any even perfect number has the form 2ⁿ⁻¹(2ⁿ − 1), it is a triangular number, and, like all triangular numbers, it is the sum of all natural numbers up to a certain point; in this case: 2ⁿ − 1. Furthermore, any even perfect number except the first one is the sum of the first 2^(n−1)/2 odd cubes:

Even perfect numbers (except 6) give remainder 1 when divided by 9. This can be reformulated as follows. Adding the digits of any even perfect number (except 6), then adding the digits of the resulting number, and repeating this process until a single digit is obtained — the resulting number is called the digital root — produces the number 1. For example, the digital root of 8128 = 1, since 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, and 1 + 0 = 1.

Odd perfect numbers

It is unknown whether there are any odd perfect numbers. Various results have been obtained, but none that has helped to locate one or otherwise resolve the question of their existence. Carl Pomerance has presented a heuristic argument which suggests that no odd perfect numbers exist. Also, it has been conjectured that there are no odd Ore's harmonic numbers (except for 1). If true, this would imply that there are no odd perfect numbers.

Any odd perfect number N must satisfy the following conditions:

• N > 10³⁰⁰. A search is currently on to prove that N > 10⁵⁰⁰.
• N is of the form

where:

• q, p₁, ..., p_k are distinct primes (Euler).
• q ≡ α ≡ 1 (mod 4) (Euler).
• The smallest prime factor of N is less than (2k + 8) / 3 (Grün 1952).
• The relation e₁≡e₂≡...≡e_k ≡ 1 (mod 3) is not satisfied (McDaniel 1970).
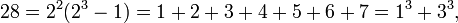
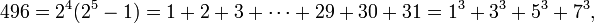
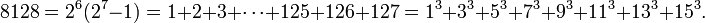
• Either q^α > 10²⁰, or > 10²⁰ for some j (Cohen 1987).
• (Nielsen 2003).

• The largest prime factor of N is greater than 10⁸ (Takeshi Goto and Yasuo Ohno, 2006).
• The second largest prime factor is greater than 10⁴, and the third largest prime factor is greater than 100 (Iannucci 1999, 2000).
• N has at least 75 prime factors and at least 9 distinct prime factors. If 3 is not one of the factors of N, then N has at least 12 distinct prime factors (Nielsen 2006; Kevin Hare 2005).
• When e_i ≤ 2 for every i
  • The smallest prime factor of N is at least 739 (Cohen 1987).
  • α ≡ 1 (mod 12) or α ≡ 9 (mod 12) (McDaniel 1970).

In 1888, Sylvester stated:

...a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number] — its escape, so to say, from the complex web of conditions which hem it in on all sides — would be little short of a miracle.

Minor results

All even perfect numbers have a very precise form; odd perfect numbers are rare, if indeed they do exist. There are a number of results on perfect numbers that are actually quite easy to prove but nevertheless superficially impressive; some of them also come under Richard Guy's strong law of small numbers:

• An odd perfect number is not divisible by 105 (Kühnel 1949).
• Every odd perfect number is of the form 12m + 1 or 36m + 9 (Touchard 1953; Holdener 2002).
• The only even perfect number of the form x³ + 1 is 28 (Makowski 1962).
• A Fermat number cannot be a perfect number (Luca 2000).
• The reciprocals of the divisors of a perfect number N must add up to 2:
  • For 6, we have 1 / 6 + 1 / 3 + 1 / 2 + 1 / 1 = 2;
  • For 28, we have 1 / 28 + 1 / 14 + 1 / 7 + 1 / 4 + 1 / 2 + 1 / 1 = 2, etc.
• The number of divisors of a perfect number (whether even or odd) must be even, since N cannot be a perfect square.
  • From these two results it follows that every perfect number is an Ore's harmonic number.
• The even perfect numbers are not trapezoidal numbers; that is, they cannot be represented as the difference of two positive triangular numbers. There are only three types of non-trapezoidal numbers: even perfect numbers, powers of two, and a class of numbers formed from Fermat primes in a similar way to the construction of even perfect numbers from Mersenne primes